固定小数点数、浮動小数点数の違いとは？IEEE754の単精度と倍精度についても解説

この記事では基本情報技術者試験を受験する人のために、テクノロジ分野で出題される、固定小数点数と浮動小数点数についてわかりやすく解説していきます。

固定小数点数とは？

固定小数点数とは、小数点を置く桁を固定して表現した数のことです。コンピュータで扱う数は桁数が32桁、64桁などと決められているため、固有小数点数では、どの桁から小数になるかを決めて数を表現します。

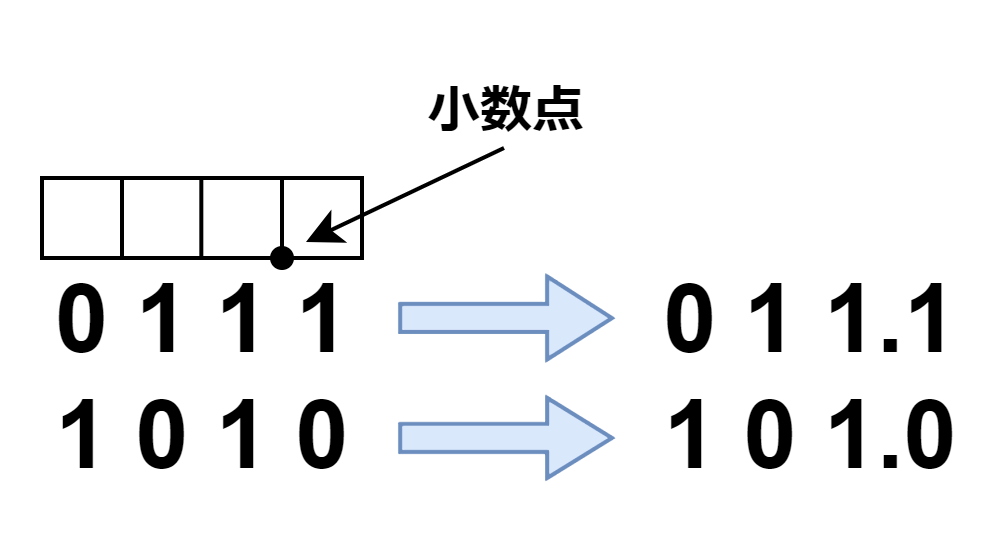
上の例では、4桁のうち下一桁が小数点以下だとすると、2進数だと0111が011.1を表していることになり、1010が101.0を表していることになります。

浮動小数点数とは？

正規化と浮動小数点数表示

不動小数点数とは、指数を用いて正規化を行い、小数点の位置を変更させて表した数のことです。では、正規化とはいったいどういうものなのでしょうか。

正規化とは、数を仮数・基数・指数分けて表記することです。

例えば、2進数の101.1は

のように正規化できます。このとき、1.011のように◯.◯◯◯と表記した部分を仮数、「2進数」の2のように各桁の重みを決める数を基数、基数を軟条するか表す数を指数と呼びます。

正規化には仮数をどう表現するかで2パターンあり、

1. $$101.1=0.1011\times2^{3}$$
2. $$101.1=1.011\times2^{2}$$

のように、0.◯◯◯と表現する方法（①）と1.◯◯◯と表現する方法（②）があります。

後に紹介するIEEE754など、ほとんどの場合は②の方を使うので、①はこういう方法もあると知っておくだけで大丈夫です。

浮動小数点数では、正規化の次に、ルールにしたがって数を表現します。ルールはいくつかありますが、代表的なものが、IEEE754です。

　

IEEE754とは？

IEEE754はIEEEが定めた浮動小数点数の標準規格です。簡単に言えば、浮動小数点数の表現のルールです。

IEEE754の単精度不動小数点数は次のように符号部、指数部、仮数部で表されます。

３つの部分はそれぞれ、

• 符号部：正負を表す。0なら正、1なら負を示す。
• 指数部：指数に127を加えた数を2進数表現で格納する。（2の補数表現ではない）
• 仮数部：仮数（1.◯◯◯）の小数点以下を格納する。

指数部は127を加えることで、0～255までの正の数で表されています。実際の指数は-127～128まで、つまり2^-127～2¹²⁸まで表すことができます。

IEEE754での正規化は②のタイブなので、仮数は1.◯◯◯となります。IEEE754の仮数部はそこから、1を除いて小数点以下の数だけ23桁で表示します。

上記は単精度浮動小数点数について考えていました。では、倍精度浮動小数点数とはなんでしょうか。

　

単精度浮動小数点数と倍精度浮動小数点数とは？

IEEE754が定める倍精度浮動小数点数とは、浮動小数点数を64bitに対応させたものです。

先程までの単精度浮動小数点数は32bitまででした。倍精度浮動小数点数はその倍の64bitになっています。

倍精度では指数部が11bit、仮数部が52bitとなり、より広い範囲の数を表すことができます。

指数部には1023を足して正規化し、仮数部は少数点以下の数だけ格納することは変わりません。

IEEE754には他にも半精度（16bit）、4倍精度（128bit）などもあります。

　

固定小数点数と浮動小数点数の違いは？

固定小数点数と浮動小数点数について上記で解説しました。この２つは小数点の表現方法が違うということがわかったと思います。

では、それぞれのメリット、デメリットはどうなっているのでしょうか。

固定小数点数は小数点の場所を決めているため、データの解釈や演算が簡単になります。しかし、その分表せる数の範囲が小さくなってしまいます。32bitの固定小数点数では、最小で2^-32、最大で2³²までしか表すことができません。

一方、浮動小数点数では、上記で見た通り、指数を2^-126～2¹²⁷まで表すことができるため固定小数点数に比べて表せる数の範囲が広いという特徴があります。しかし、正規化を行って小数点の位置がずれるためデータの演算がしにくい、誤差が出やすいといった欠点もあります。

　

例題

例題として、次の浮動小数点数表示の2進数を10進数になおしてみましょう。

• 符号部：1より符号はマイナス
• 指数部：131から127を引いて指数は4
• 仮数部：1を加えて、1.0101

よって2進数を10進数になおすと、

$$-1.0101\times2^{4}=-10101=-21_{(10)}$$

となります。

　

まとめ

固定小数点数と浮動小数点数の違いやIEEE754の倍精度、単精度について解説しました。

浮動小数点数はちょっと複雑なので計算練習が必要かもしれません。